Delegating to the saturated pool is less profitable

Wealth is distributed unequally in society and there is a trend that a large portion of wealth is held by a small fraction of the population. For example, Pareto distribution power-law states that, for example, 80% of the wealth of a society is held by 20% of its population. This distribution is undesirable within PoS protocol since a few wealthy stakeholders could become powerful and only a few entities could obtain the right to produce a new block. In a decentralized system, everybody should have the ability to contribute and participate in making consensus. Staking pool allows combining user’s stakes and the creation of a single entity. Pool’s stake consists of a pool’s operator stake and stakes of all users that have delegated their coins to the pool. Users can whenever delegate to other pools if they are not satisfied with the pool for any reason.

If you ask what is a desirable decision power distribution then the answer would be the most decentralized one. The economic incentives should be configured in a way that ensures fair coexistence of many pools with similar size.

Both the stake of pool operators and delegators determines the sizes of pools. It can happen that there will be a whale in the system that has a 5% stake. It would be also desirable to economically motivate the whale to distribute the stake into smaller portions.

In Proof-of-Work (PoW) the rewards are distributed proportionally to the size of pools. If a pool has a portion of 15% of the total hashing power of the network then it mines approximately 15% of new blocks so it gets 15% of rewards. However, this proportional rewarding approach does not support a high level of decentralization. As we can observe, there are often only a few bigger pools in PoW projects and the number decreases as time passes. PoW pool gets the higher reward the bigger the pool becomes and there is no limitation. To prevent centralization in PoW there must be people who put aside economic interests and delegate hash-rate to the less profitable pool for other reasons. The question is how it is probable in reality.

Saturation point

The linearity between pool size and rewards must be interrupted at some point. Linearity is good for smaller pools but must decrease as pools begin to gain dominance. Based on the pool size, Cardano divides rewarding behavior into two stages. The first one is a growth stage where the linearity in rewarding is respected. The second stage is a stabilization stage where the pool is considered as large. The large pool is thus considered as saturated.

When a pool reaches a saturation point the protocol will cut rewards. If the saturation point is 1% of all staked coins, then the pool that has 1,5% of staked coins will have the same reward as a pool that has 1% of staked coins.

When a pool becomes saturated?

Let’s have a look at how the saturation point can be found.

First of all, we have to know how many ada coins are used for consensus, in other words, how many coins are staked. There is a certain amount of coins in circulation, however, only a part of them is used for staking. It can be 10% or 90%. It is hard to predict since some coins can be used for other purposes. It can be expected that ada holders will want to participate in consensus and receive rewards. The number of staked coins will change in time (in each epoch) so the exact saturation point cannot be calculated in advance.

Let’s assume that 10 000 000 000 ada coins are staked. There will be a desirable number of pools in the network that will be defined in the protocol by a constant K. It is a desirable number of pools, no limitation or max amount of pools. If there is a desirable number of pools set to 1000, then K = 1000.

Saturation point can be then calculated in the following way:

Saturation-point ≥ Staked-ada-coins / K

In our case:

Saturation-point ≥ 10 000 000 000 / 1000

In our example, a pool gets to the saturation point when it holds stake ~10 000 000 ada.

Notice that a pool can be saturated regardless of a number of pools in the network. It does not matter that the desired number of pools is set to 1000 and there are actually only 250 pools. In this scenario, a pool can be also saturated. So if the desired number of pools in the network is not reached and there are saturated pools then less reward is distributed meaning that not all coins prepared as a reward are not used. There is an economic potential to join the network and try to get these unused coins. It motivates people to participate and create new pools up to the desired number of pools.

The constant K influences also the maximum reward a pool can receive in an epoch.

Max-reward = pot / K

For example, there can be prepared fix amount of ~3 800 000 ada coins as a reward for each epoch (pot). Let’s have a look at maximum possible reward per pool in an epoch:

Max-reward = 3 800 000 / 1000

In each epoch, a pool can obtain maximum reward 3 800 ada coins.

It is more profitable to delegate coins to not saturated pool

Let’s have a look at a nice example that we have found in IOHK blog:

To appreciate how the dynamics work from the perspective of a single stakeholder, consider the following example. Suppose there are two pools, A and B managed by Alice and Bob, with operational costs of 25 and 30 coins respectively, each one with a profit margin of 4%. Suppose further that the total rewards to be distributed are 1,000 coins and the saturation point of the reward-sharing mechanism is 20%. At a given point in time, Alice’s pool has 20% of the stake, so it is at the saturation point, while Bob’s pool is at 19%. A prospective pool member, Charlie, holds 1% of the stake and considers which pool to join. Joining Alice’s pool will bring its total stake to 21%, and because it has exceeded the saturation point the reward will be 200 coins (20% of the total rewards). Deducting operational costs will leave 175 coins to be distributed between Alice and the pool members. After removing Alice’s profit margin and considering Charlie’s relative stake in the pool, he will receive 8 coins as a reward. If Charlie joins Bob’s pool, the total rewards will be 200 coins, or 170 coins after removing the operational costs. However, given that Charlie’s stake is 5% (1/20) of the pool, it turns out that he will receive 2% more coins than if he had joined Alice’s pool. So Charlie will join Bob’s pool if he wants to maximize his rewards.

Now, let us see what happens in the case that Charlie is facing the same decision at a hypothetical earlier stage of the whole process when Alice’s pool was already at 20% of the total stake, while Bob’s pool was only at 3%. In this case, Bob has a very small pool and the total rewards available for its members are much less compared with the previous case. As a result, if Charlie did the same calculation for Bob’s pool, his 1% stake would result in a 4% total stake for the pool but, if one does the calculations, he would receive a mere 30% of the rewards that he would have obtained had he joined Alice’s pool. In such a case, the rational decision is to join Alice’s pool despite the fact that his membership will make Alice’s pool exceed the saturation point.

Shelley test-net calculations

In Shelley test-net, the desired number of pools is set to 100 and a reward prepared for epochs is ~3 800 000 ada coins. Total staked ada coins were nearly 9 000 000 000 at the moment of writing the article. Let’s calculate the saturation point.

Saturation-point ≥ 9 000 000 000 / 100

A pool is saturated when it reaches 90 000 000 staked ada. What is the maximum pool’s reward per epoch?

Max-reward = 3 800 000 / 100

Maximum pool’s reward is 38 000 ada coins.

Examples

Let’s have a look at examples using Adapools.org tool that shows pools statistics including average ROI. We checked rewards in the last 5 epochs for two pools that have similar fees (no tax-fix and tax-ratio 5%).

Check Adapools.org:

Cardano staking pools

We will be constantly improving it and if the data provided is useful to you and you want to support further…

adapools.org

As you can see the first pool is saturated since it had ~500M ada coins and the operator decreased the amount to ~280M ada coins in the actual epoch in order to increase ROI. As you can see in the actual epoch ROI is 3.7%.

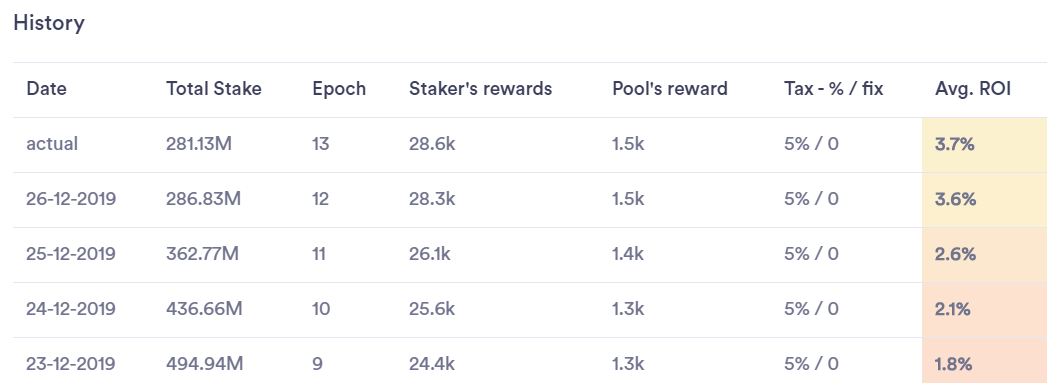
The pool below is not saturated since it has a stake that is below 90 M ada coins. ROI is 13.4 in the actual epoch.

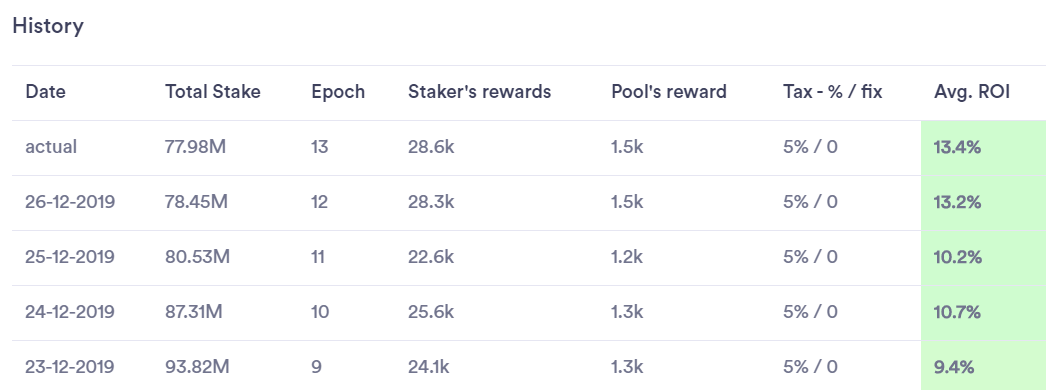
It is more profitable to delegate ada coins to the second pool.

If you would like to learn how pool operator fees work read our article:

How Cardano pool operator fees work

The Cardano Shelley incentivized test-net has been launched and people can delegate their ada coins to the selected…

medium.com

Summary

If you want to maximize your profit you have to find an appropriate pool. We strongly propose you to use Adapools.org tool that allows you to find all important data about pools.

The profitable pool from the view of delegators is one that is not saturated and the pool’s stake is not too low (slowly approaching to saturation), has fair fees and is able to produce blocks since only a pool that produces blocks is rewarded by the protocol.

It is not always only about profit and users might have other incentives to delegate coins to some pools. For example, some pool operators might use the reward to give it back to the ecosystem.

Good luck!